The Soma
Google Search of SETI Net
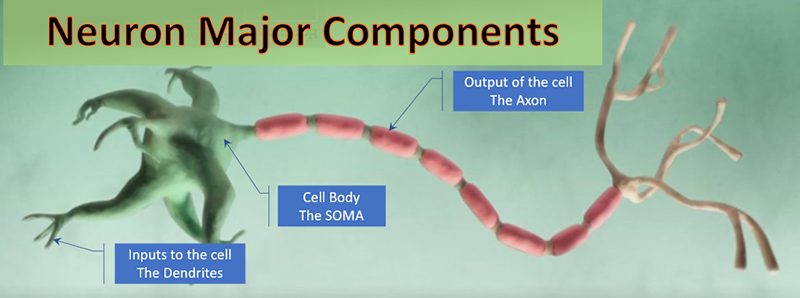
The Soma
The Soma is the spherical central part of the neuron It is typically about 20 um in diameter and contains a salty potassium solution inside the cell. It is separated by the neural membrane as described earlier. Contained inside the Soma are a number of very important structures called organells but these are ignored in this simulator.
The neuron Soma is the physically largest part of the neuron. It typically has a diameter of 100 uM. The diameter of the dendrites may be down to 1 uM or less. The dendrites usually extend 100's of microns, but some can extend several meters, as in the giraffe brain.
Many thousands of Inputs to the Soma arrive from the Dendrites. Its single output is the Axon
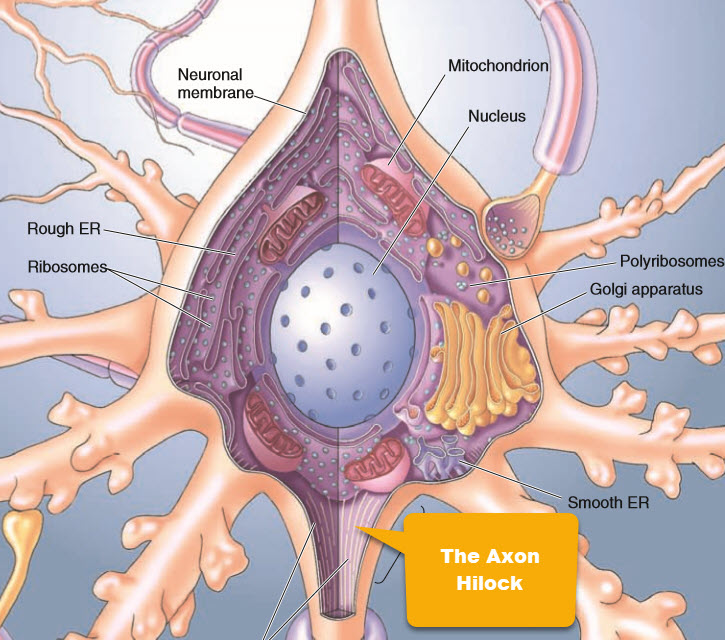
The key feature of the Soma is its ability to initiate an Action Potential in the area labeled the Axon Hillock (shown above). The spiking process starts in the Hillock also called the spike-initiation zone.
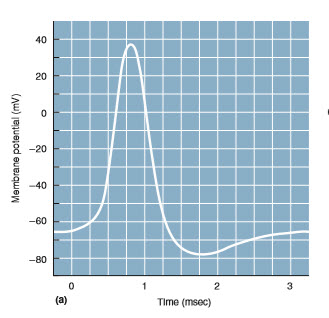
A typical action potential or spike is shown below.
Membranes of dendrites and the Soma body do not generate action potentials because they have very few voltage-gated sodium channels. Only the Soma hillock and the Axons are capable of generating action potentials.
The cell body of the typical neuron is about 20 µm in diameter.[Bear Fig 2.7]
Distance is not a factor in the propagation of a signal in the neuron’s soma ecause the cell body can be approximated as a sphere whose membrane voltage is uniform.[Kandel Fig 9 - 10]
The Action Potential profile begins at the membrane rest potential (about - 60 mV) and rises rapidly in the depolarization phase toward 0 mV. It overshoots the mark and then reverses back down to the resting potential. It then overshoots that and moves to the hyperpolerized region and then recovers to the resting potential. A drawing of this process is shown in section 2 Ionic Currents (near the bottom).
The software model used in this simulator is based on Dynmical Systems in Neuronscience by Izhikevich. It is not based upon biophysical parameters but is a model that faithfully reproduces all the neurocomputational dynamical features of the neuron. The model is a two-dimensional systems having a fast voltage variable v and a slower “recovery” variable u, which describes activation of the K+ current or inactivation of the Na+ current or their combination. The model can reproduce spiking and bursting behavior of many known types of neurons and is described by a pair of differential equations
Those two equations make up a model called a Quadratic Integrate-and-fire neuron. In the Neuron Simulater this is implemented (in the Delph language) with this code:
Vout := Vin + tau * (k * (Vin - Vr) * (Vin - Vt) - Uin + i) / CAP; Uout := Uin + tau * a * (b * (Vout - VRest) - Uin); if Vout >= vpeak then begin Vout := c; Vin := vpeak; // Reset the membrane Uout := Uout + d; // Reset the recovery variable end;
Where:
- Vout = The current millisecond step calculated membrane potential [mV]
- Vin = The last membrane potential at step -1 [mV]
- Uout = The current calculated recovery value
- Uin = The calculated recovery value at step -1
- tau = Step time between samples
- Cap = 100 Membrane capacitance [pF]
- Vr = -60 Resting membrane potential [mV]
- Vt = -40 instantaneous threshold potential. Above this a spike will occure [mV]
- k = 0.7 Parameters used for RS type
- a = 0.03 ; Recovery time constant [ms]
- b = -2.0 Constant [pA/ohm]
- c = -50 Membrane voltage reset
- d = 100 ; For a neocortical pyramidal neuron
The numeric values for k,a,b,c, and d vary by the type of neuron being simulated.
The threshold potential (Vt) is neuron type dependent and my be viewe or changed in the main menu (Setup | Neuron Select). The capacitance (Cap) is size dependant. A suggested Cap is shown for the selected Neuron. This can be varied by changing the Dimensions of the Soma (right click).
The soma (or cell body) of a neuron varies in size depending on the type of neuron and its location in the nervous system. Here's the general range for length and diameter:
Soma Diameter (or Width)
-
Typical Range:
4 µm to 100 µm -
Most common range:
10 µm to 50 µm - Small neurons (e.g., granule cells): ~4–10 µm
- Large neurons (e.g., spinal motor neurons): 50–100 µm
Soma Length (if not spherical)
- Many somas are roughly spherical or oval, so "length" and "diameter" may be similar. But for asymmetrical cells:
- Length range: ~10 µm to 100 µm
-
Width/diameter may differ slightly depending on orientation

Eugene Izhikevich founder and CEO Brain Corp. San Diego
You may chose different neuron types in the simulator through the Setup | Neuron Select menu.
Selecting the Cat Chattering Neuron type:
